· The end behavior of a function is the behavior of the graph of the function f (x) as x approaches positive infinity or negative infinity This is determined by the degree and the leading coefficient of a polynomial function For example in case of y = f (x) = 1 x, as x → ± ∞, f (x) → 0 graph {1/x 10, 10, 5, 5} But if y = f (x) = 3x2 · If you were to get the slope of f (x) at the far left it would be increasing 1, 2, 3 and peaking at 4 around x = 75 Then decreasing to 3, 2, 1, 0 Note that those decreasing values 3, 2, 1 are still positive Again its not easy to see just looking at f (x) but the graph of f ' (x) makes it clear Hope that helps!On what interval is f decreasing?
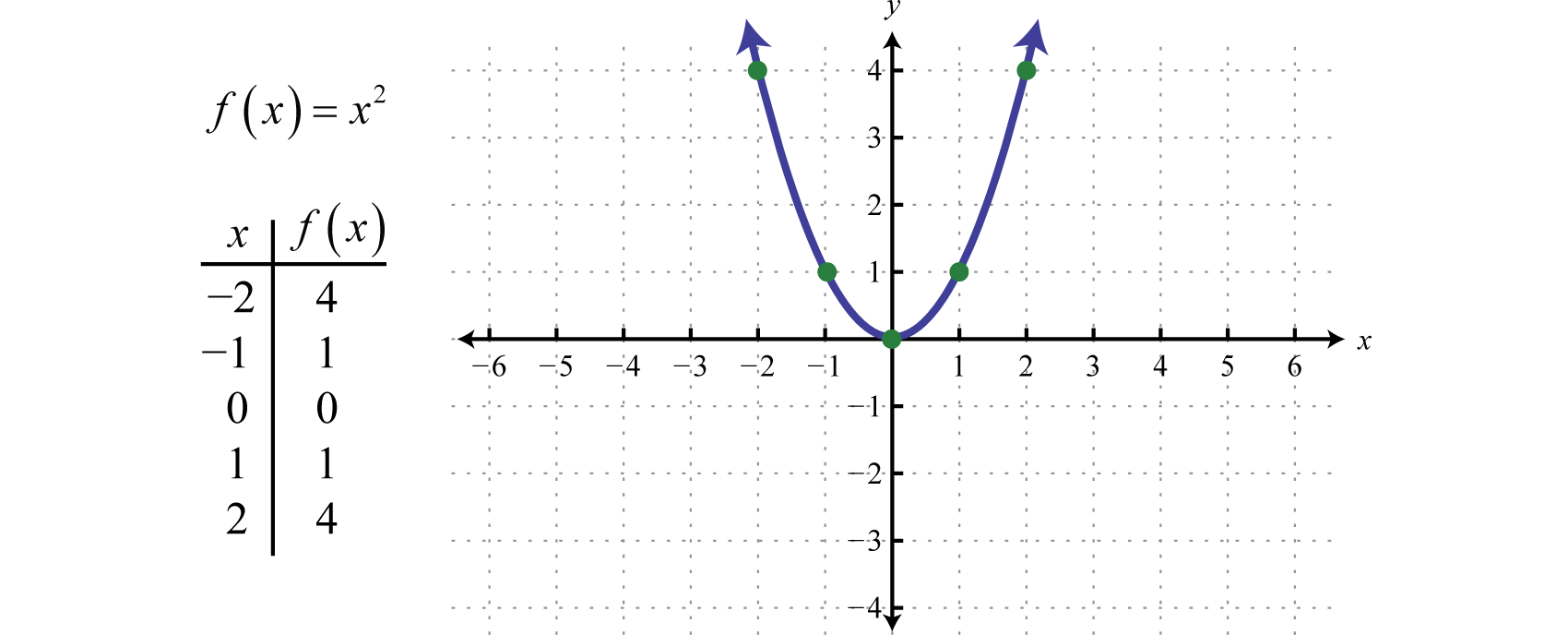
Quadratic Functions And Their Graphs

