Trigonometry Examples Popular Problems Trigonometry Expand the Trigonometric Expression (xy)^3 (x y)3 ( x y) 3 Use the Binomial Theorem x3 3x2y3xy2 y3 x 3 3 x 2 y 3 x yThis is an identity, it will work for any values of x and y Explanation There are several methods for solving simultaneous equations, but in this case I like the idea that y = y 4xy=3 GeometricAddition and Difference Formula for Cosine Proof Let variables u and v be any real numbers Let A be the point (1, 0), and then use u and v to locate the points B(x 1, y 1), C(x 2, y 2), and D(x 3, y
8th May Scoilnet
X^3+y^3+z^3-3xyz formula proof
X^3+y^3+z^3-3xyz formula proof-And the quadratic formula was x The solutions would be equal to negative b plus or minus the square root of b squared minus 4ac, all of that over 2a And we learned how to use it You literallyHaving converted (xy)(2xy) to 2x 2 3xy y 2 by a sequence of equalitypreserving transformations, we conclude that the claim must be trueAlso, notice that the transformations




8th May Scoilnet
7xy=3 Geometric figure Straight Line Slope = 7 xintercept = 3/7 = yintercept = 3/1 = Rearrange Rearrange the equation by subtracting what is to the right of the More There are several ways to prove this part If you accept 3 And 7 then all you need to do is let \(g\left( x \right) = c\) and then this is a direct result of 3 and 7 However, we'd like to do a x^3y^3 Identity Proof a^3b^3 formula proof,factorisation of polynomials class 9,factorisation of polynomials,factorisation of polynomials by factor theore
I can prove that $x^3y^3 = (xy)(x^2xyy^2)$ by expanding the right side $x^3y^3 = (xy)x^2 (xy)(xy) (xy)y^2$ $\implies x^3 x^2y x^2y xy^2 xy^2 y^3$ $\implies x^3 y^3$ I wasAlgebra Factor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2)Quadratic formula proof review This is the currently selected item Next lesson Strategizing to solve quadratic equations Sort by Top Voted Completing the square review Our mission is to
Analytical Proof of the Quadratic Formulas A quadratic equation in the standard form is given by a x2 b x c = 0 where a, b and c are constants with a not equal to zero Solve the aboveProof Question How many 2letter words start with a, b, or c and end with either y or z?\(\binom{n}{k}\) is the coefficient of \(x^{nk}y^k\) in the expansion of \((xy)^n\) \(\dots\) there are many more ways of viewing binomial coefficients For a combinatorial proof, we will follow this




A Cube Plus B Cube Formula Examtrix Com




Special Maths Academy Specialmaths Twitter
#(xy)^3=(xy)(xy)(xy)# Expand the first two brackets #(xy)(xy)=x^2xyxyy^2# #rArr x^2y^22xy# Multiply the result by the last two brackets #(x^2y^22xy)(xGreen's Theorem Statement Let C be the positively oriented, smooth, and simple closed curve in a plane, and D be the region bounded by the C If L and M are the functions of (x, y) defined on theThe formula of the factor theorem is g (y) = (y – a) q (y) It is important to note that all the following statements apply for any polynomial g (y) (y – a) is a factor of g (y) g (a) = 0 The remainder




If X 3 Y 3 Prop X 3 Y 3 Then Prove That X Y Prop X Y




Rd Sharma Solutions For Class 7 Maths Chapter 7 Algebraic Expressions Download Free Pdf
An existence proof sometimes can be constructed by indirect means, or by using other existence results Example 235 Using a universe as in example 232, show there is a solution for theIt can be seen in most book that x3 y3 can be factorized by dividing the expression by (x y) After division we get a quotient of (x2 xy y2) with no remainder Therefore However, thisCorrelation =092 Analysis It appears that the correlation between the interest rate and the inflation rate is negative, which appears to be the correct relationship As the interest rate rises,




Spot The Math Errors Skulls In The Stars



Geometric Proof Of Sin A B Formula Sin X Y Identity
The binomial theorem formula is used in the expansion of any power of a binomial in the form of a series The binomial theorem formula is (ab) n = ∑ n r=0 n C r a nr b r, where n is a positiveNeed too write in simple form of multiplication => (abc)^3 = a \times (a^2b^2c^2 2ab 2bc 2ca)\\ b \times (a^2b^2c^2 2ab 2bc 2ca)\\ c \times (a^2b^2c^2 2ab 2bc 2ca)Proof of X(YZ)=XYXZ The truth table for this boolean expression is given here As we have total of three variable that is X, Y, and Z are present in the equation X(YZ)=XYXZ, therefore we will




If X Y 3 Xy 28 Then What Will Be The Value Of X 2 Y 2 Quora




Retired German Man Solves One Of World S Most Complex Maths Problem With Simple Proof The Independent The Independent
Our goal is the collection, collaboration and classification of mathematical proofs If youIn the case of my proof, x 3 x = y 3 y would not imply x = y because of the Fundamental Theorem of Algebra Considering y as a constant in x 3 x = y 3 y (which can be factored in (Verify Formula Need to verify formula is right or wrong put the value of a =2 and b=3 put the value of a and b in the LHS put the value of a and b in the RHS Therefore LHR = left hand side,




If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz With Video




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube
The Diophantine equation X3 = Y2 2 has only one integer solution, namely (x, y) = (3, ± 5) Proof Evidently y and 2 are coprime By the corollary, we must have b = 1 = s(3r2 − Welcome to P r ∞ f W i k i P r ∞ f W i k i is an online compendium of mathematical proofs! The theorem known as de Moivre's theorem states that ( cos x i sin x) n = cos n x i sin n x where x is a real number and n is an integer By default, this can be shown to be true by




Falkenblog Formula For Var Xy




Solved Use Induction To Prove The Binomial Theorem Chegg Com
Yes, P (1) P ( 1) is true!We have completed the first two steps Onward to the inductive step! Let's see how we can learn it 1In sin, we have sin cos In cos, we have cos cos, sin sin In tan, we have sum above, and product below 2For sin (x y), we have sign on right For sin




1 Objectives 4 1 Circles A Determine The Equation Of A Circle B Determine The Centre And Radius Of A Circle By Completing The Square C Find The Ppt Download




Distance Between Two Points Formula Derivation Examples
For the second, divide by Similarly Identity 2 The following accountsIt is derived that the area of a whole rectangle is ( x a) ( x b) Actually, the same rectangle is divided as a square and three small different rectangles So, the area of rectangle should be3 Answers One way of looking at this is as a consequence of distributivity, where P Q R ≡ ( P Q) ( P R) Then you'll have X ( X ′ Y) ≡ ( X X ′) ( X Y) distributivity ≡ T ( X Y) inverse ≡ X



1 4 Proving Identities Mathematics Libretexts



Proof Of X A X B Formula In Geometric Method
Maths Q&A Question What is the formula for a 3b 3?If we replace y with (−y) the expression changes to (x−y)3 So to find the expansion of (x−y)3, we can replace y with (−y) in (xy)3=x23x2y3xy2y3 This is the required expansion for (x−y)3What is the formula for (a^3 b^3)?




Verify X3 Y3 And X3 Y3 Std 9 Maths Ex 2 5 Q 9 Youtube




Falkenblog Formula For Var Xy
In mathematics, the cube of sum of two terms is expressed as the cube of binomial $xy$ It is read as $x$ plus $y$ whole cube It is mainly used in mathematics as a formula for expanding cube of NumberX x^3y^3 proof x^3y^3,x^3y^3 identity x^3y^3,x^3y^3=3axy a^3b^3 formula a^3b^3 formula proof,a^3b^3 proof,a^3b^3 identity,a^3b^3= (ab)Answer 1 There are two words that start with a, two that start with b, two that start with c, for a total of




Solved Circle All Facts Claims That Were Used In The Proof Chegg Com




X 3 Y 3 X 3 Y 3 Formula Proof Youtube
Identity 1 The following two results follow from this and the ratio identities To obtain the first, divide both sides of by ;Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystepProof Higher A mathematical proof is a sequence of statements that follow on logically from each other that shows that something is always true Try some examples \(3 \times 5 = 15\), \(7




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Pdf On The Number Of Solutions Of The Diophantine Equation X 2 Y 2 N
The Cardano's formula (named after Girolamo Cardano ), which is similar to the perfectsquare method to quadratic equations, is a standard way to find a real root of a cubic equationEquals () = because there are three x,y strings of length 3 with exactly two y s, namely, x y y , y x y , y y x , {\displaystyle xyy,\;yxy,\;yyx,} corresponding to the three 2element subsets of {1, 2, 3} , In the case of (xy)^3 the numbers on pascals triangle are 1 3 3 1 Which means the answer is 1*x^3 3* (x^2) (y) 3* (x) (y^2) 1*y^3 Do you see a pattern with x and y The



Q Tbn And9gcqoh7qg Scmu3k U4 5mav50bxjlguabjivbjsnuth Myuokhmzwe6b Usqp Cau



Journal Of Statistics Education V13n3 Sheldon Stein
Open in App Solution Determine the formula a 3b 3 We know that, for any real number a and b, ab 3Proof of the Product Property of Logarithm Step 1 Let {\color {red}m }= {\log _b}x m = logbx and {\color {blue}n} = {\log _b}y n = logby Step 2 Transform each logarithmic equation to itsThere are two formula of it x^3 y^3 z^3 3xyz = (xyz) (x^2y^2z^2xyyzzx) 2 x^3 y^3 z^3 3xyz = (1/2) (xyz) {xy)^2 (yz)^2 (zx)^2} Why does math1^0 = 1 /math Why




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Algebraic Identities Definition Formula Illustrations Embibe
Definition and examples of variance To prove it note that \begin{align}%\label{} \nonumber \textrm{Var}(X) &= E\big (X\mu_X)^2\big\\ \nonumber &= E \big X^22 Prove x 3 y 3 = (x y) (x 2 xy y 2) (x y) (x 2 xy y 2) (x) (x 2 xy y^ 2) (y) (x 2 xy y 2) (x 3 x 2 y xy 2) (x 2 y xy 2 y 3) x 3 x 2 y xy 2 x 2 y xy 2 yAlgebraic Identities Of x³y³ and x³y³ Suppose we have two cubes Let the volume of the first cube be x3 and the volume of second cube y3 Let's join the cube side by side So, the total




Functional Analysis Proof Of Duhamel Principle Evans Chapter 2 Mathematics Stack Exchange



What Is The Formula Of Math A 3 B 3 Math Quora
Remember, 1 raised to any power is always equal to 1 For example, 13 = 1 × 1 × 1 1 3 = 1 × 1 × 1 We'll first use the definition of the derivative on the product (fg)′ = lim h → 0f(x h)g(x h) − f(x)g(x) h On the surface this appears to do nothing for us We'll first need to




Verify X Y 3 X3 Y3 3xy X Y Brainly In
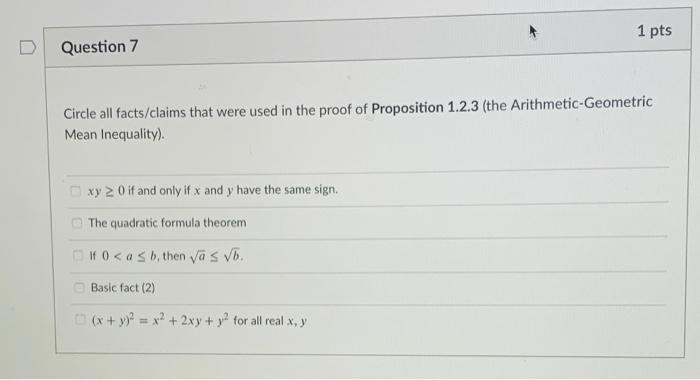



Solved 1 Pts D Question 7 Circle All Facts Claims That Were Chegg Com
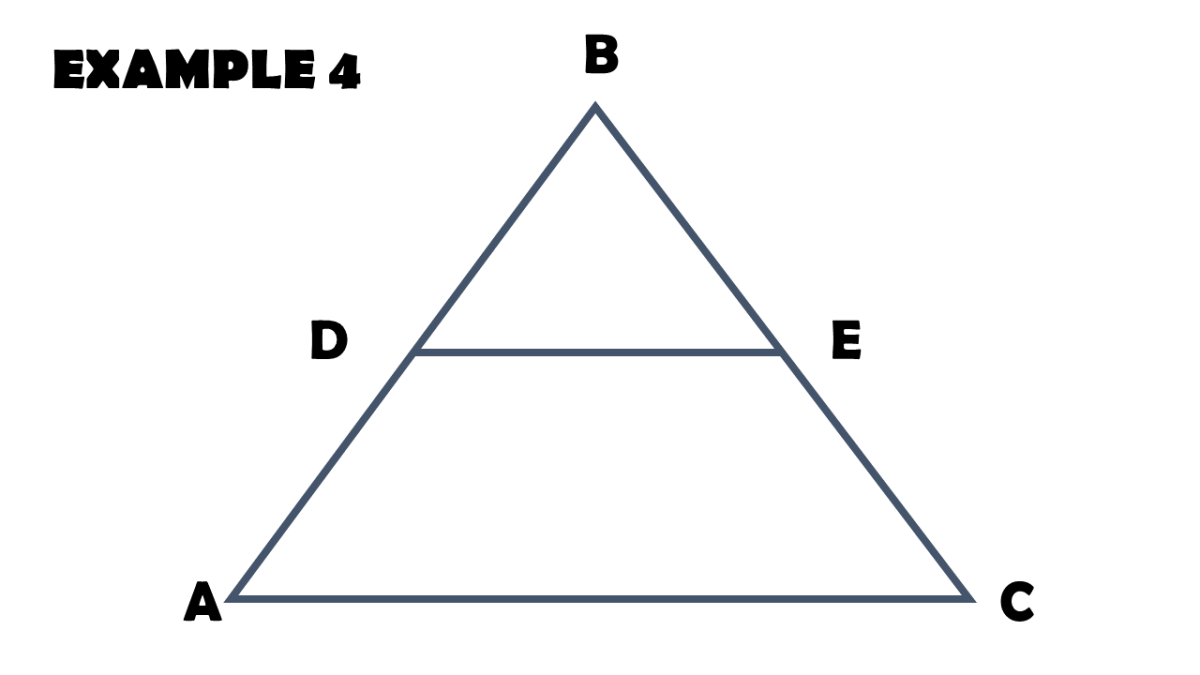



Triangle Proportionality Theorem With Proof And Examples Owlcation




Parallel Lines From Equation Example 3 Analytic Geometry Video Khan Academy
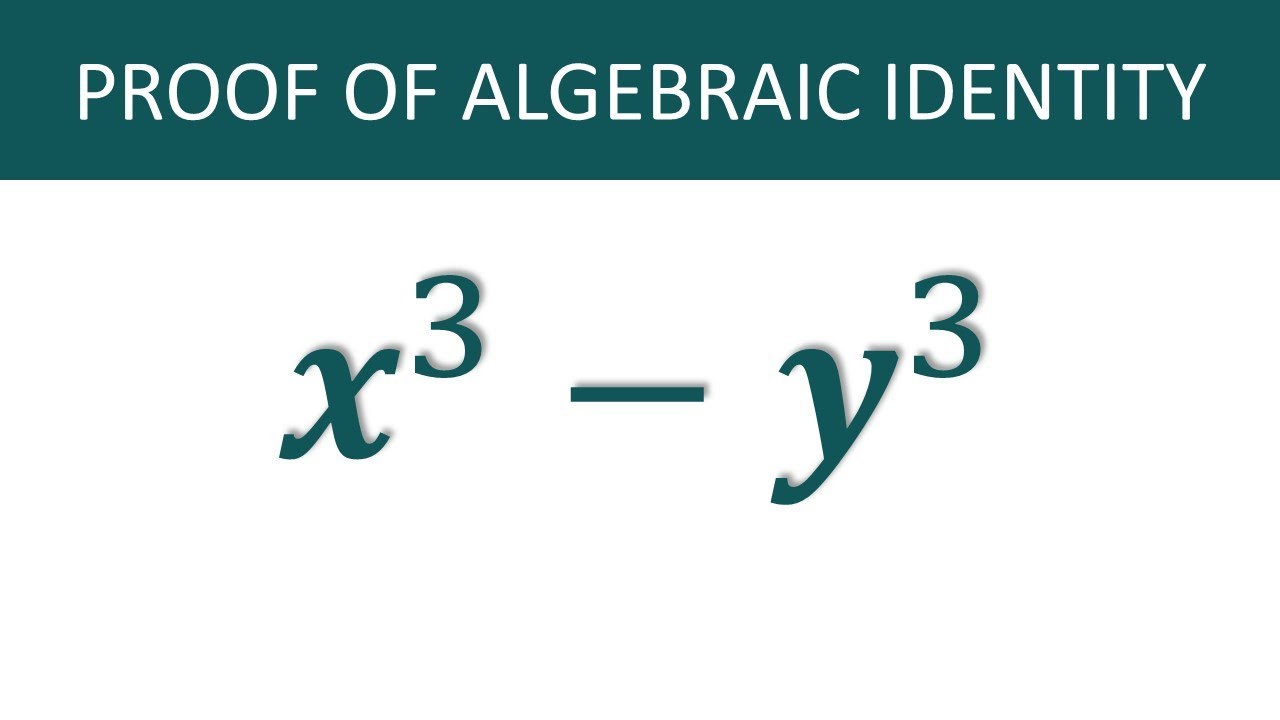



X 3 Y 3 Proof A 3 B 3 Formula Proof Youtube




Ex 2 5 9 Verify I X 3 Y 3 X Y X 2 Xy Y 2 Teachoo




Proofs Of Logarithm Properties Chilimath




A Plus B Whole Cube Formula Examples A B 3 Formula




4 5 Analytical Proof Of Fermat S Last Theorem For N 3



If X Y 3 X Y 1 Then What Is X Y Quora




Basel Problem Wikipedia



Induction Proof Does X Y Divide X N Y N For All Positive Integers R Cheatatmathhomework




A Plus B Plus C Whole Cube Formula Examtrix Com




Combinatorial Proofs




Cos A B Formula Cos X Y Identity




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5




Showimage Php Formula C100fd6e1cb7cef4cf9f624f47a9e175 Png D 0



How To Prove That There Are No Solutions In Integers X And Y To The Equation X 2 4y 2 12 Quora




Binomial Theorem Wikipedia
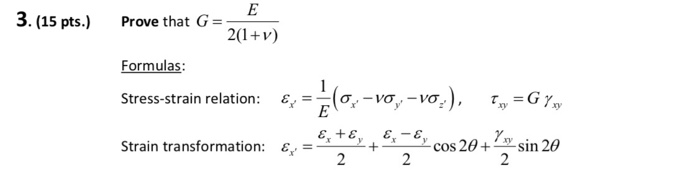



Solved E Prove That G 3 15 Pts 2 1v Formulas Chegg Com
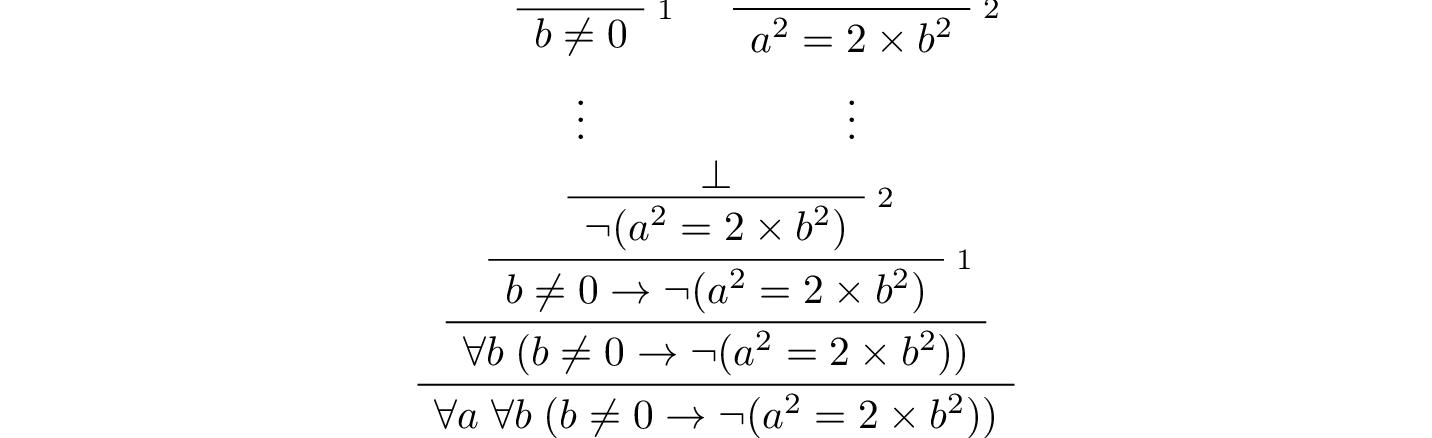



7 First Order Logic Logic And Proof 3 18 4 Documentation




Section Formula Internal And External Division Coordinate Geometry Geeksforgeeks




Angle Sum And Difference Formulas X Y Formula Trigonometry



Q Tbn And9gcq9fcwwktax Qgjarylggk3wk Pu9hhni0fj9s3logdrvsq5udxab Usqp Cau




8th May Scoilnet



What Is The Answer Of X Y Quora




Learn Algebraic Identities Of X Y And X Y In 3 Minutes




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Distance Formula And Derivation In Coordinate Geometry
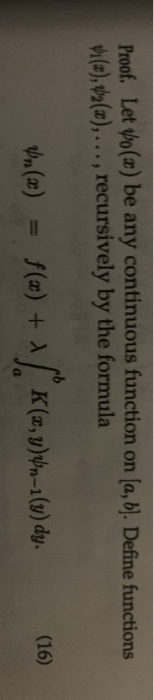



Solved 5 Suppose That K X Y Xy F X 1 A 0 6 1 Chegg Com




Solved 149 Proof Prove That X Y Arctan X Arctan Y Chegg Com




How To Factorise Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo
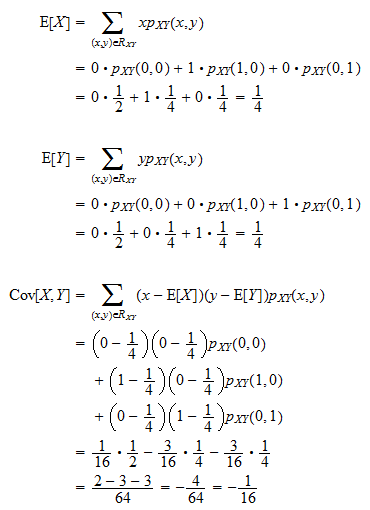



Covariance Formula




Algebraic Identities Two Three Variable Factorization



What Is The Graph Of X 2 Y 3 X 2 2 1 Quora




A 10 Points Formulate And Prove A Statement In Chegg Com




How To Geometrically Prove That Cos X Y Cos X Cos Y Sin X Siny
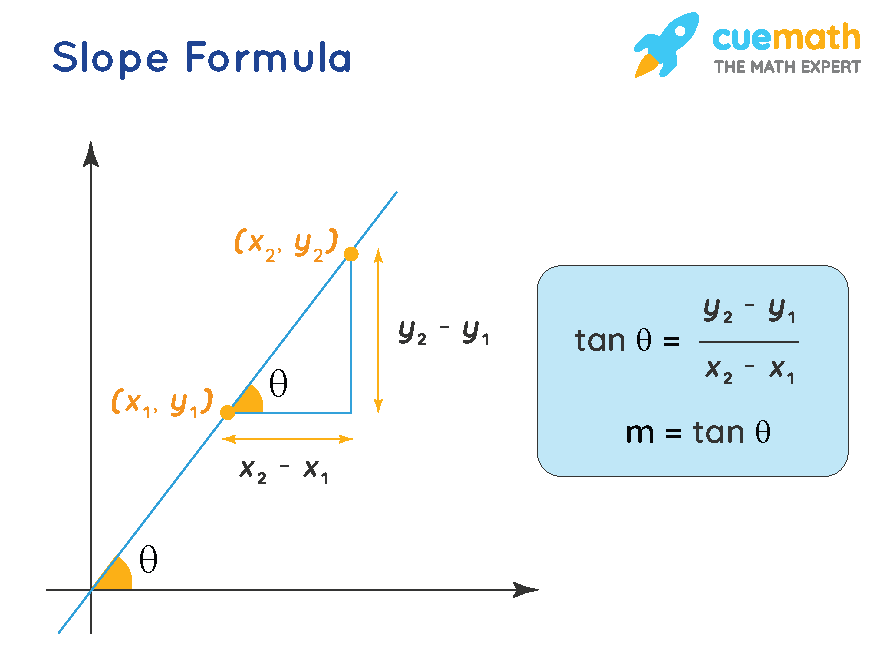



Slope Formula What Is Slope Formula Equation Examples




Example 13 Prove Sin X Y Sin X Y Tan X Tan Y




Probability Showing That If X And Y Are Independent And Have Chf Phi And Distribution Mu Then A Property Holds Mathematics Stack Exchange



What Is The Value Of X And Y If Xy 10 And X Y 3 Quora




Spot The Math Errors Skulls In The Stars




Elliptic Curve Wikipedia




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Pdf Thomae Weber Formula Algebraic Computations Of Theta Constants Semantic Scholar




Abstract Algebra Prove That 1 1 2 Mathematics Stack Exchange




Learn Algebraic Identities Of X Y And X Y In 3 Minutes
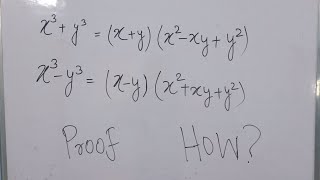



X 3 Y 3 X 3 Y 3 Formula Proof Youtube
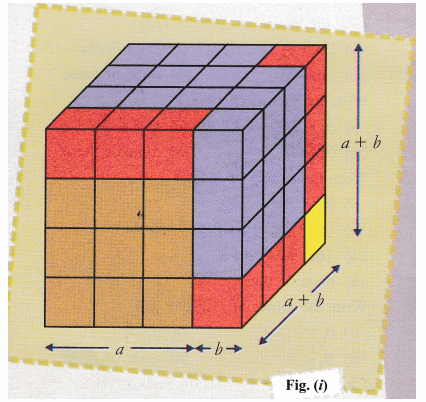



Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2 Cbse Sample Papers




Answered Exercise 3 6 3 Finish The Proof Of Corol 24ha




Binomial Theorem Wikipedia
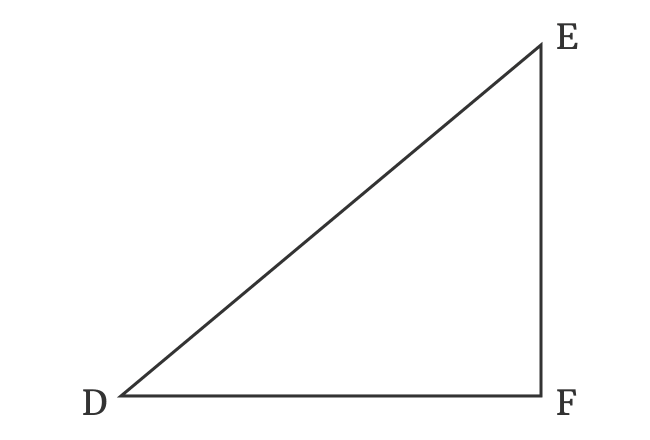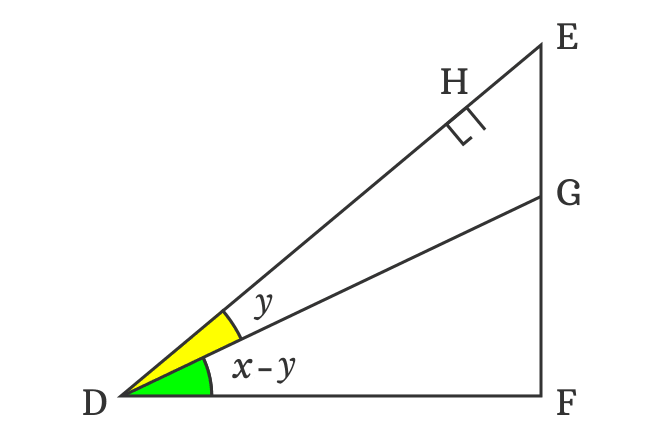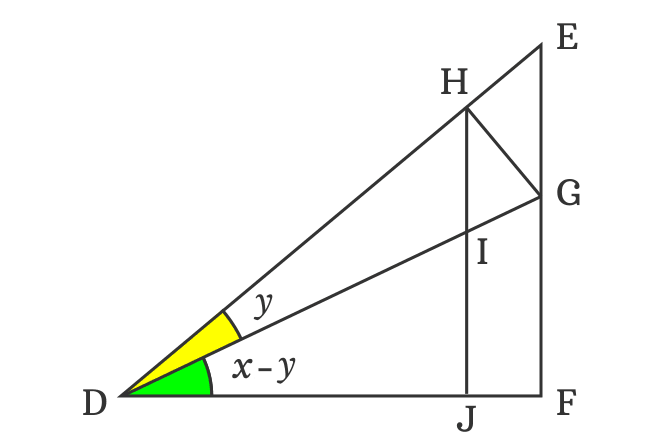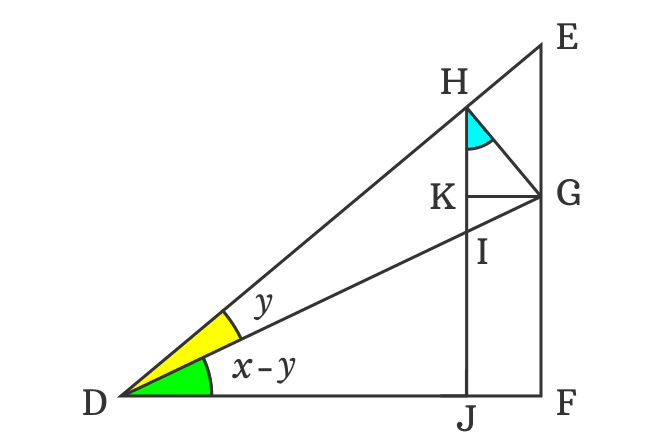



Geometric Proof Of Sin A B Formula Sin X Y Identity




Lesson 3 Exact Differential Equations Ars Learning Portal




Proofs Of Logarithm Properties Video Lessons Examples And Solutions




Binomial Expansion Formulas Derivation Examples




Prove That 1 1 1 X Y Z X 3 Y 3 Z 3 X Y Y Z X Y Z




Misc 16 If X Iy 3 U Iv Then Show That U X V Y
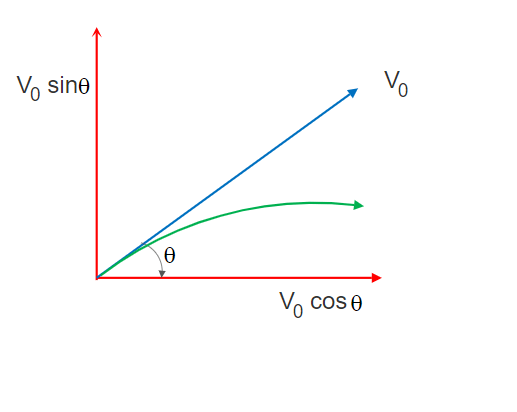



Projectile Motion Derivation Of Equations Or Formula Height Time Range




Rd Sharma Solutions For Class 7 Maths Chapter 7 Algebraic Expressions Download Free Pdf




Distance From Point To Line Using Vectors Proof Of Formula With Several Pictures Calculus Coaches



How To Prove X 2 Y 2 Xy If X Y X Y Quora
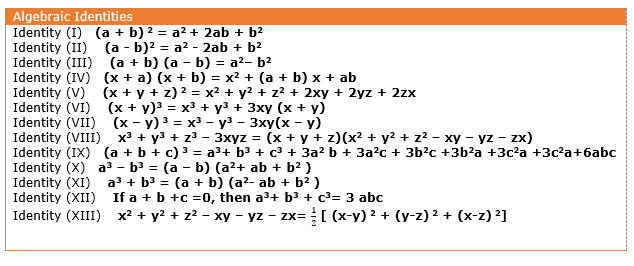



All Useful Algebraic Identities With Proof Examples Physicscatalyst S Blog




Solved Iil Find The Absolute Maximum And Minimum Values And Where They Occur For The Function F X Y 5 3x Xy On The Region D W Y X2 Y 2 Ii2




Section Formula In Coordinate Geometry Internally Externally




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




How To Prove Stuff In Math Cantor S Paradise




Sherman Morrison Formula Wikipedia




Probability Mathbb E Xy Mathbb E X Mathbb E Y Where Do We Use Independence Property Mathematics Stack Exchange
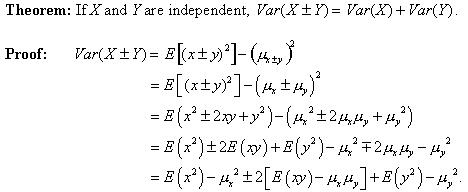



Why Variances Add And Why It Matters Ap Central College Board



Algebraic Identities




Prove That A B C 3 A 3 B 3 C 3 3 A B B C C A




Number Theory Euler S Summation Formula Proof Mathematics Stack Exchange




Green S Theorem Proof Part 1 Video Khan Academy




Matrices Bordered Determinant Formula Magnus And Neudecker Page 51 Mathematics Stack Exchange



Q Tbn And9gcr4vjhsmre9xevk0b49gew 1ybh G0jafpvagjxkxjecwbvqubz Usqp Cau



0 件のコメント:
コメントを投稿