Double this for a denominator of 4a Put them together, and this gives you the formula for kAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsA quadratic function is a function of degree two The graph of a quadratic function is a parabola The general form of a quadratic function is f(x) = ax2 bx c where a, b, and c are real numbers and a ≠ 0 The standard form of a quadratic function is f(x) = a(x − h)2 k The vertex (h, k

Write The Quadratic Function In The Form F X Chegg Com
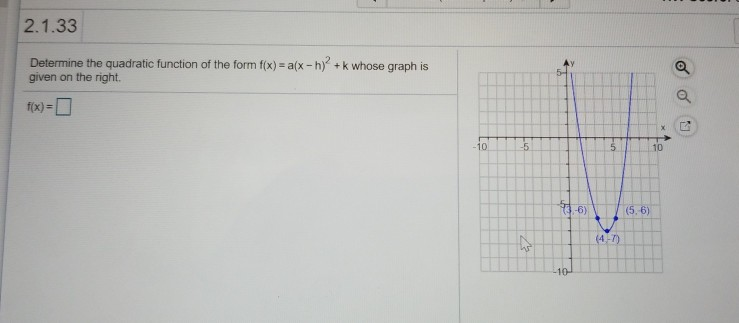
Determine the quadratic function of the form f(x)=a(x-h)^2+k
Determine the quadratic function of the form f(x)=a(x-h)^2+k-We want to put it into vertex form y=a(xh) 2 k;Vertex form vertex axis of symmetry Describe the following functions in terms of position, direction of opening, and width compared to its parent function 1 y = 2(x 1)2 3 2 y = 9(x 3)2 3 f(x) = 05x2 1 4 y = x2 PULL




Vertex Intercept And Standard Form Read Algebra Ck 12 Foundation
0=a (xh)2k No solutions found Rearrange Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation 0 (a* (xh)^2k)=0 Write the quadratic function in the form g (x)= a (xh)^2 k Write the quadratic function in the form g(x) = a(x−h)2 k https//mathstackexchangecom/questions//writethequadraticfunctionintheformgxaxh2kGraphing f (x) = a(x − h)2 k The vertex form of a quadratic function is f (x) = a(x − h)2 k, where a ≠ 0 The graph of f (x) = a(x − h)2 k is a translation h units horizontally and k units vertically of the graph of f (x) = ax2 The vertex of the graph of f (x) = a(x − h)2 k is (h, k), and the axis of symmetry is x = h h f(x) = ax2 y x f(x) = a(x − 2h) k k (h, k)Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor
Our equation is in standard form to begin with y=ax 2 bxc;1 Introduction The composition of two functions g and f is the new function we get by performing f first, and then performing g For example, if we let f be the function given by f(x) = x2 and let g be the function given by g(x) = x3, then the composition of g with f is called gf and is worked outAnswer by robertb(5643) (Show Source)
An alternate approach to finding the vertex is to rewrite the quadratic function in the form f (x) = a (x − h) 2 k When in this form, the vertex is (h, k) and can be read directly from the equation To obtain this form, take f (x) = a x 2 b x c and complete the square A quadratic function is a function of degree two The graph of a quadratic function is a parabola The general form of a quadratic function is f(x) = ax2 bx c where a, b, and c are real numbers and a ≠ 0 The standard form of a quadratic function is f(x) = a(x − h)2 kQuestion This question is from textbook solving quadratic functions of the form f(x)=a(xh)2k(that 2 is a squared) i know how to get the value of a,h,k, but i dont know what they mean when they say choose some values for x in example 1 they have 7 values for x, but in example 2 they have 5 values for x so how do you know how many numbers to chose forthe value of x?




How To Write Quadratic Functions Video Lesson Transcript Study Com



Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 a2 17 unit 2 2 ws packet lg Pdf
The general form of quartics of this form is y = a(x −h)4 k The turning point is at (h,k) When sketching quartic graphs of the form y = a(x − h)4 k, first identify the turning point To add further detail to the graph, the xaxis and yaxis intercepts are found Example 2 Sketch the graph of the function y = (x − 2)4 − 1Solution for Write the function in f(x) = a(x − h)2 k form Determine the vertex and the axis of symmetry of the graph of the function f(x) = 9x2 54x36 is the value for 'c' that we found to make the right hand side a perfect square trinomial




Quadratic Function Wikipedia
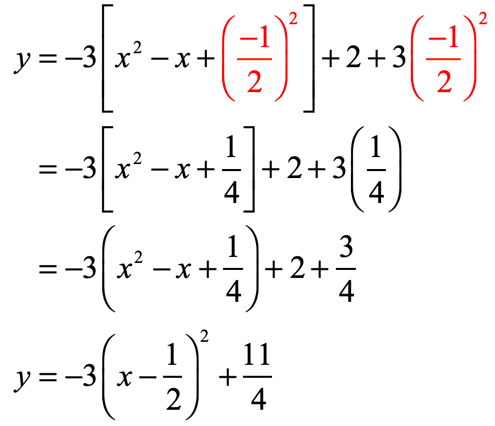



Completing The Square Step By Step Chilimath
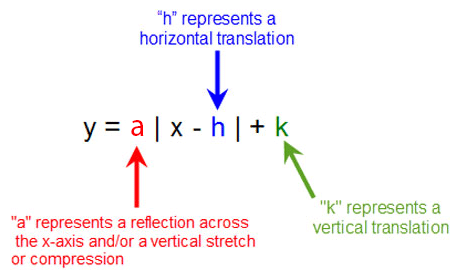
The function p(x) = –8x2 – 64x can be written in vertex form p(x) = a(x – h)2 k, where a =, h =, and k = To graph the function p, reflect the graph of f(x) = x2 across the xaxis, vertically stretch the graph by a factor of 8, shift the graph units, and then shift the graph unitsPlugging these values into the general form f(x) = a f b(x − h) k where f(x) = , we get f(x) = 4 3 This can be simplified to f(x) = 3 _____ The mapping rule is useful when graphing functions with transformations Any point (x, y) of a parent function becomes ( h, ay k)The vertex form of a quadratic is given by y = a(x – h) 2 k, where (h, k) is the vertex The "a" in the vertex form is the same "a" as in y = ax 2 bx c (that is, both a's have exactly the same value) The sign on "a" tells you whether the quadratic opens up or opens down



Solved Use The Vertex H K And The Point On The Graph Xy To Find The Standard Form F X A X H 2 K Of This Equation Quadratic Function Course Hero



Illustrative Mathematics
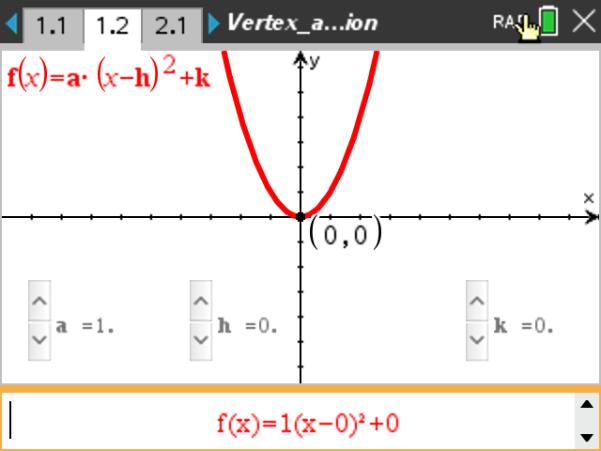
F(x)=a(x−h)2k{\displaystyle f(x)=a(xh)^{2}k\,\!}is called the vertex form, where hand kare the xand ycoordinates of the vertex, respectively The coefficient ais the same value in all three forms To convert the standard formto factored form, one needs only the quadratic formulato determine the two roots r1and r2Parabolas The Vertex Form of a Parabola The formula for the vertex form of a parabola is f(x) = a(x h)2 k where a = vertical stretch or shrink of the parabola and (h, k) are the (x, y) coordinates of the vertex of the parabola h = the xcoordinate and k = the ycoordinateSo let's put that into this form of the equation f (x) = a (xh)2 k f (x) = a (x−1)2 1 Then we calculate "a" We know the point (0, 15) so f (0) = 15 And a (x−1)2 1 at x=0 is f (0) = a (0−1)2 1 They are both f (0) so make them equal a (0−1)2 1 = 15 Simplify a 1 = 15 a = 05



For The Following Problem Find The Quadratic Chegg Com




Transform The Following Quadratic Function Into The Vertex Form F X A X H 2 K And Identify The Brainly Ph
The discriminant in the Quadratic Formula is b 2 – 4ac Take the negative of this to get the reverse of the subtraction –(b 2 – 4ac) = 4ac – b 2 The formula for h has a denominator of 2a;F (x) = a(x h) 2 k, where (h, k) is the vertex of the parabola FYI Different textbooks have different interpretations of the reference " standard form " of a quadratic function Some say f ( x ) = ax 2 bx c is "standard form", while others say that f ( x ) = a ( x h ) 2 k is "standard form" Write the function in the form $f(x)=a(xh)^{2}k$ by completing the square Then identify the vertex $$q(x)=2 x^{2}12 x11$$



In The Following Exercises Write The Quadratic Function In F X A X H 2 K Form Whose Graph Is Shown Bartleby




Mathematics Learners Material Module 2 Q
Express f(x) in the form a(xh)^2 k f(x)= x^24x8 Thank You!!!We can convert to vertex form by completing the square on the right hand side;Write the function f(x) = x 2 6x 7 in standard form Sketch the graph of f and find its zeros and vertex f(x) = x 2 6x 7 = (x 2 6x ) 7 Group the x 2 and x terms and then complete the square on these terms = (x 2 6x 9 9) 7 We need to add 9 because it is the square of one half the coefficient of x, (6/2) 2 = 9 When we



Graphing Quadratic Equations In Vertex Form Walk Around Activity Lv 2 Scavenger



Graph By Transformations F X A X H 2 K Youtube
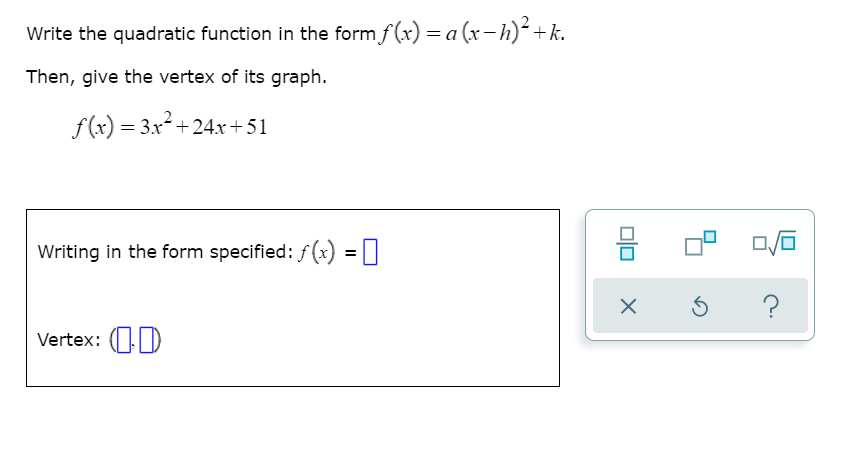
Answer to Write the quadratic function in the form f(x)= a(x h)^2 k Then, give the vertex of its graph f(x)= 2x^2 4x 4 By signing up, tex\bf \qquad \textit{parabola vertex form}\\\\ \begin{array}{llll} y=a(x{{ h}})^2{{ k}}\\\\ x=a(y{{ k}})^2{{ h}} \end{array} \qquad\qquad vertex\ ({{ hIn analytic geometry, the graph of any quadratic function is a parabola in the xyplaneGiven a quadratic polynomial of the form the numbers h and k may be interpreted as the Cartesian coordinates of the vertex (or stationary point) of the parabolaThat is, h is the xcoordinate of the axis of symmetry (ie the axis of symmetry has equation x = h), and k is the minimum value (or




How To Graph A Quadratic Equation 10 Steps With Pictures




The Vertex Form Of A Quadratic Function Is F X A X H 2 K What Is The Vertex Of Each Function Brainly Com
Vertex form is defined as #f(x)=a(xh)^2k# The way to find the vertex is to use #b/(2a)# (for the #h# value), and then plug that number in for #x# in the original quadratic (for the #k# value) Now that we know that, we can solve for our #h# value #b/(2a) => (3)/(2(5)) => 3/10# Now that we have our #h# value, we can plug it in for #x# in the quadraticQuestion Write The Quadratic Function In The Form F(x) = A(xh)^2 K Then, Give The Vertex Of Its Graph F(x) = 2x^2 16x 35 This problem has been solved!MATH EXPRESSING A QUADRATIC FUNCTION KSU IN STANDARD FORM Deflnitions † Quadratic function is a function that can be written in the form f(x) = ax2 bxc where a;




Ex Write Ax 2 Bx C In The Form A X H 2 K Negative A Youtube



Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora
Intermediate Algebra (4th Edition) Edit edition Solutions for Chapter 75 Problem 18PE Write the function in the form f(x) = a(x h2) k by completing the square Then identify the vertex (SeeExamples 1–2)h(x) = x2 4x 5The vertex form of a parabola is another form of the quadratic function f(x) = ax 2 bx c The vertex form of a parabola is f(x) = a(x h) 2 k The a in the vertex form of a parabola corresponds to the a in standard form If a is positive, the parabola will open upwards If a is negative, the parabola will open downwardsThis video shows how to use vertex form ie y = a(x h)² k to graph a parabola or use it to write an equation from a graph This lesson was created fo




Graphing Parabolas




2 4 Quadratic Functions Ppt Download
Solution for f (x)=a (xh)2k equation Simplifying f (x) = a (x 1h) * 2 k Multiply f * x fx = a (x 1h) * 2 k Reorder the terms fx = a (1h x) * 2 k Reorder the terms for easier multiplication fx = 2a (1h x) k fx = (1h * 2a x * 2a) k fx = (2ah 2ax) k Solving fx =The figure shows a graph of the function $f(x)=x^2$ a) For each of the graphs of quadratic functions below, find values of $a$, $h$, and $k$ so that the function $fSee the answer Show transcribed image text Expert Answer 100% (1 rating) Previous question Next question Transcribed Image Text from this Question
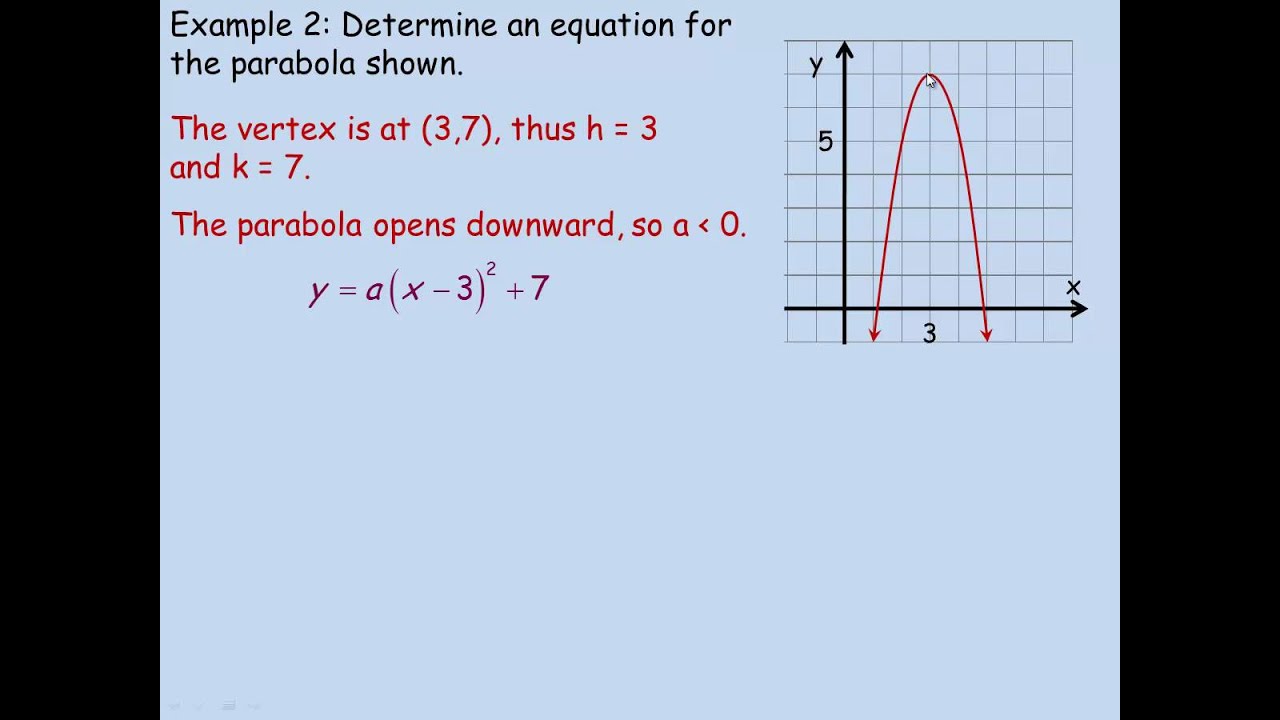



Graphing Y A X H K Youtube



1
The standard form of a quadratic function presents the function in the form latexf\left(x\right)=a{\left(xh\right)}^{2}k/latex where latex\left(h,\text{ }k\right)/latex is the vertex Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function The standard form is useful for determiningAny quadratic function can be written in the standard form f (x) = a (x h) 2 k where h and k are given in terms of coefficients a, b and c Let us start with the quadratic function in general form and complete the square to rewrite it in standard form Given function f (x) f (x) = ax 2 bx c Express the right hand side as a square f(x)4 = (x1)^2 Step 5 Isolate f(x) f(x) = (x1)^24 The equation is now in vertex form y = a(x – h)^2 k, where (h, k) is the vertex h = 1 and k = 4, so the vertex is at (1,4)




Quadratic Functions
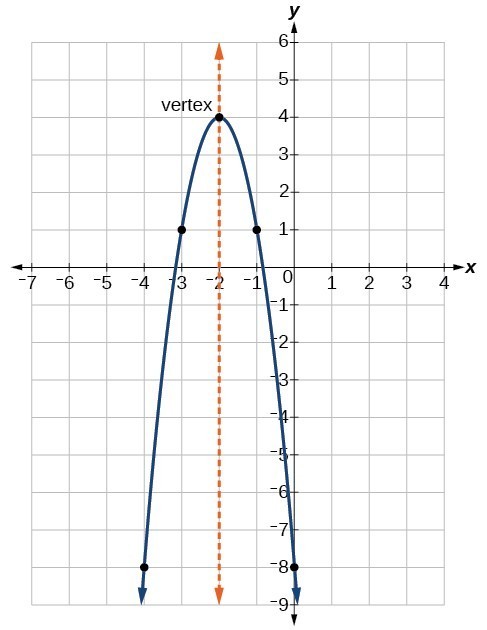



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra
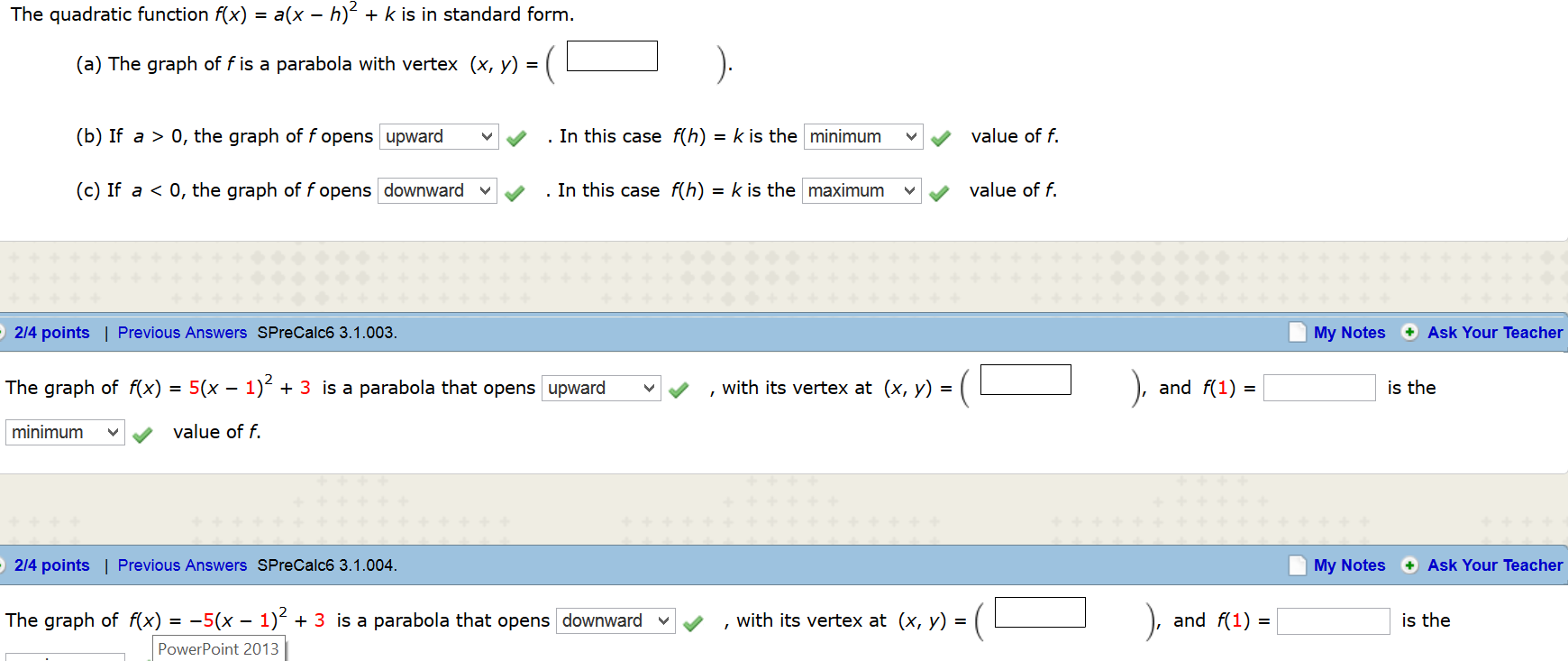
Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeF(x) = a(x h) 2 k The term (x h) 2 is a square, hence is either positive or equal to zero (x h) 2 ≥ 0 If you multiply both sides of the above inequality by coefficient a, there are two possibilities to consider, a is positive or a is negative case 1 a is positive a(x h) 2 ≥ 0 Add k to the left and right sides of the inequality a(x h) 2 k ≥ kHe quadratic function f(x)=a(xh)^2k is in standard form (a) The graph of f is a parabola with vertex (x, y) = (_____) (b) If a > 0, the graph of f opens upward/downward In this case f(h) = k is the (maximum/minimum)value of f (c) If a < 0, the graph of f opens (upward/downward) In this case f(h) = k is the (maximum/minimum)value of f
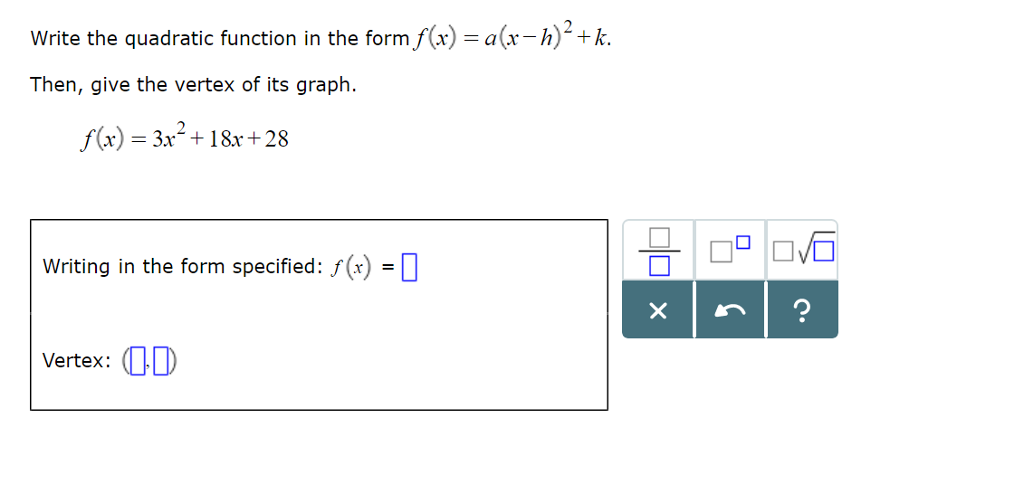



Write The Quadratic Function In The Form F X Chegg Com




Quadratic Functions
The focus of this paper is to determine the characteristics of parabolas in the form y = a(x h) 2 k For our purposes, we will call this second form the shiftform equation of a parabola Given a quadratic in this form, it is fairly easy to predict the general shape of the parabola By examining a coefficient and the values for h and k, itF(x) = x^24kx(311k) where k is a constant 1 (I have no problem with this question but i'll just mention it) Express f(x) in the form (xp)^2 q, where p andq are constants to be found in terms of kThe simplest exponential, the general form, is defines as f(x)=2 x However, as you probably know from previous experience, graphs are generally not this friendly and simple They can shift, flip, and change in shape depending on coefficients and other values applied to the general form
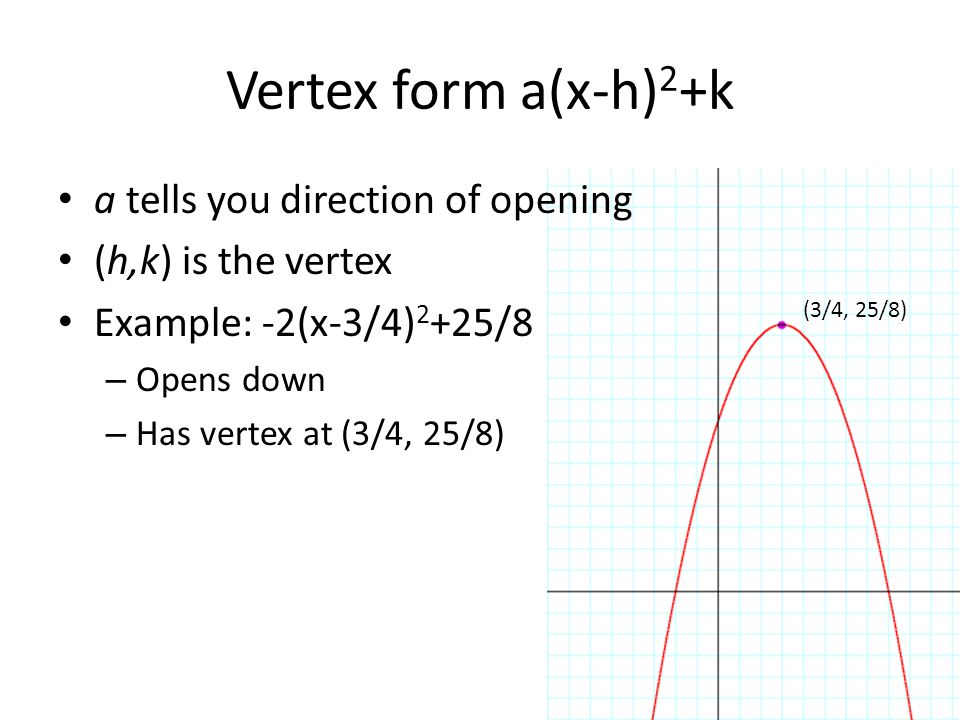



Vertex Form Ppt Download




The Graph Of F X X 2 Has Been Shifted Into The Form F X X H 2 K What Is The Value Of H A 1 B Brainly Com
f(x) = a(x − h)2 k form Determine the vertex and the axis of symmetry of the graph of the function f(x) = x2 4x − 5B, and c are real numbers and a 6= 0 † Parabola The graph of a squaring function is called a parabola It is a Ushaped graph † Vertex of a parabola The point on the parabola where the graph changes
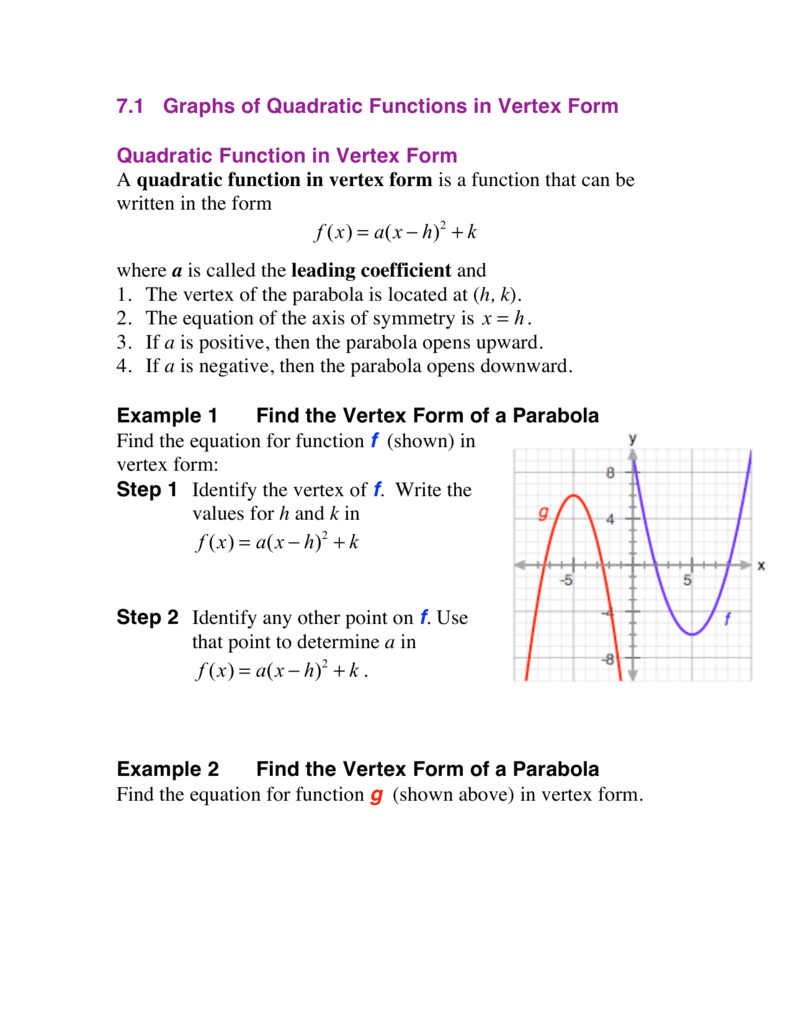



F X A X H 2 K F X A X H 2 K F X A X H 2 K




Quick Review Before Hw Quiz Y A X H 2 K Form Vertex H K Axis X H Up If A 0 Down If A 0 Ex Y X 1 2 4 Y 1 X 1 2 4 A 1



Staffweb Psdschools Org Eharding Alg1v Bigideasch 8 A1v8 4notesgraphingf A Xh K Pdf




The Graph Of F X Ax 2 All Quadratic Functions Have Graphs Similar To Y X 2 Such Curves Are Called Parabolas They Are U Shaped And Symmetric With Ppt Download




Also Identify The Vertex No Need To Sketch Write The Quadratic Function In A X H 2 K Form Hint Homeworklib
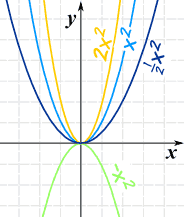



Graphing Quadratic Equations




Finding Features Of Quadratic Functions Video Khan Academy
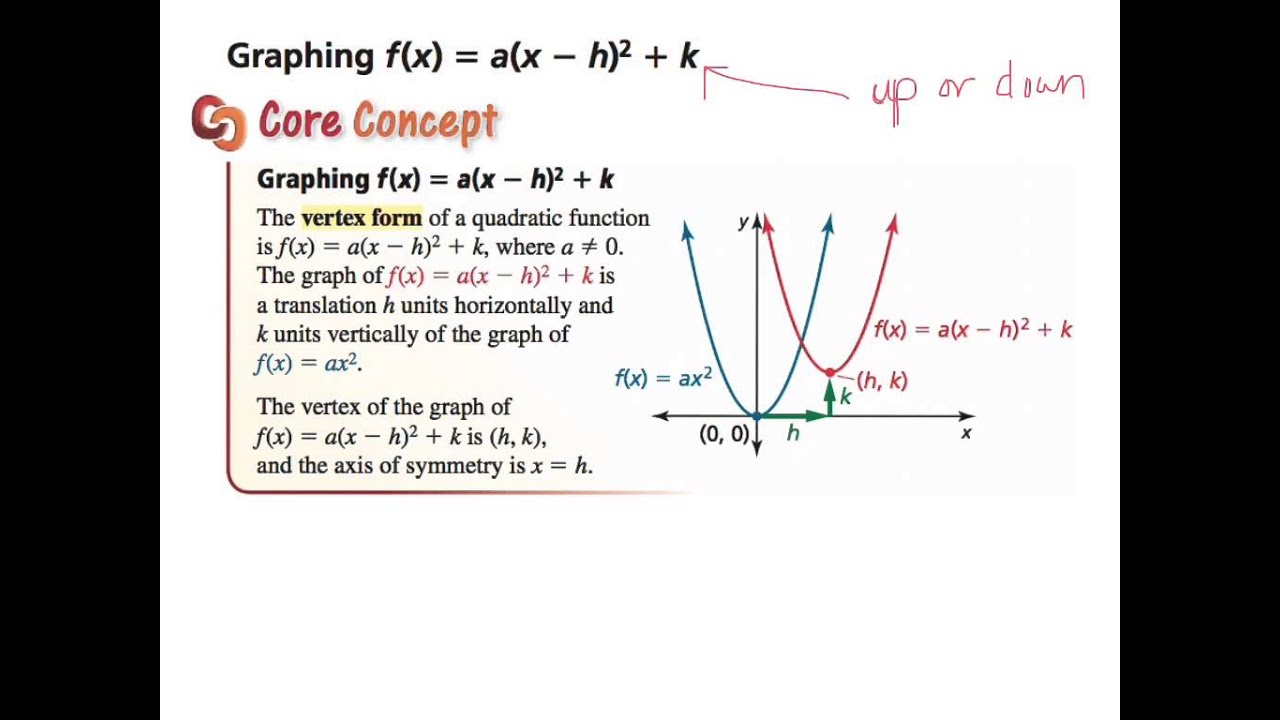



7th Section 8 4 Graphing F X A X H 2 K Youtube



Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora




Ch 7 Tutoring Notes Quadratics
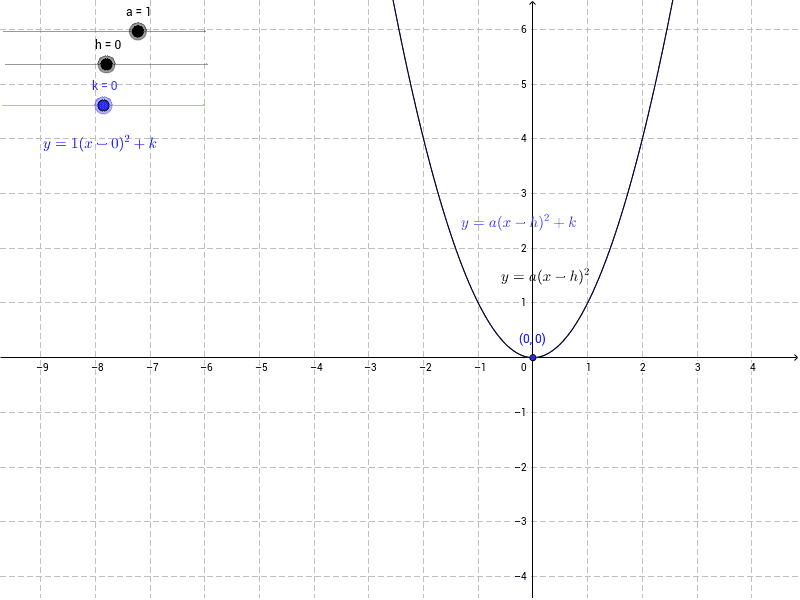



Investigating The Graph Of Y X H 2 K Geogebra




What Is Vertex Form Example Get Education
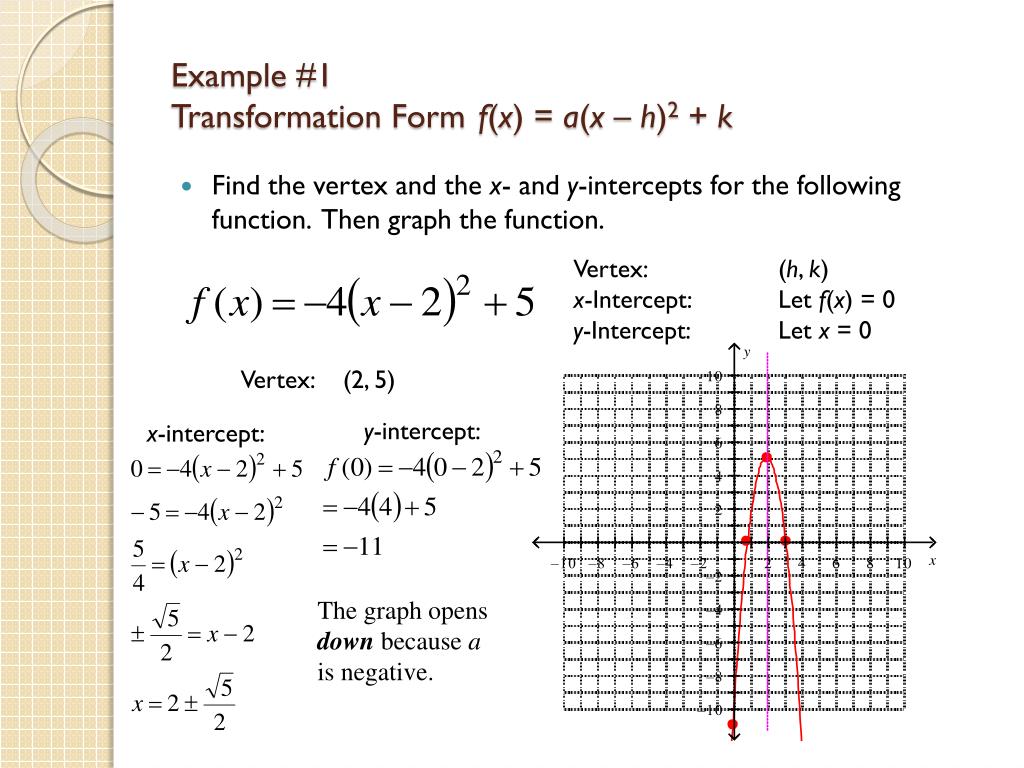



Ppt 3 3 Quadratic Functions Powerpoint Presentation Free Download Id



Sections 6 And 8 Quadratics Part 2 And Polynomial Functions




Quadratic Functions Ppt Download




Quadratic Functions




How To Graph A Quadratic Equation 10 Steps With Pictures



Solution Write The Quadratic Function In The Form F X A X H 2 K Find The Vertex And Graph The Function A F X X 2 6x B F X X 2 4x 1 C F X 3x 2 10x 2




Transform The Following Quadratic Functions In The Form F X A X H 2 K Determine The Values Of A H Brainly Ph



Graphing Quadratics Vertex Form Algebra Video Khan Academy




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21



Vertex Form Of Quadratic Equation Mathbitsnotebook A1 Ccss Math




Graphing Parabolas



Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 a2 17 unit 2 2 ws packet lg Pdf




The Following Graph Of F X X2 Has Been Shifted Into The Form F X X H 2 K Brainly Com



Www Hackensackschools Org Site Handlers Filedownload Ashx Moduleinstanceid 1615 Dataid Filename Vertex form transformations notes day 1 Pdf




The Vertex Form Of A Quadratic Function Is F X A X H 2 K What Is The Vertex Of Each Function Brainly Com




Quadratic Functions
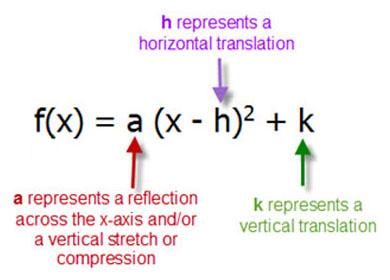



Untitled Document




3 Ways To Find The Maximum Or Minimum Value Of A Quadratic Function Easily




Quadratic Functions Ppt Download



Search Q Axis Of Symmetry Tbm Isch
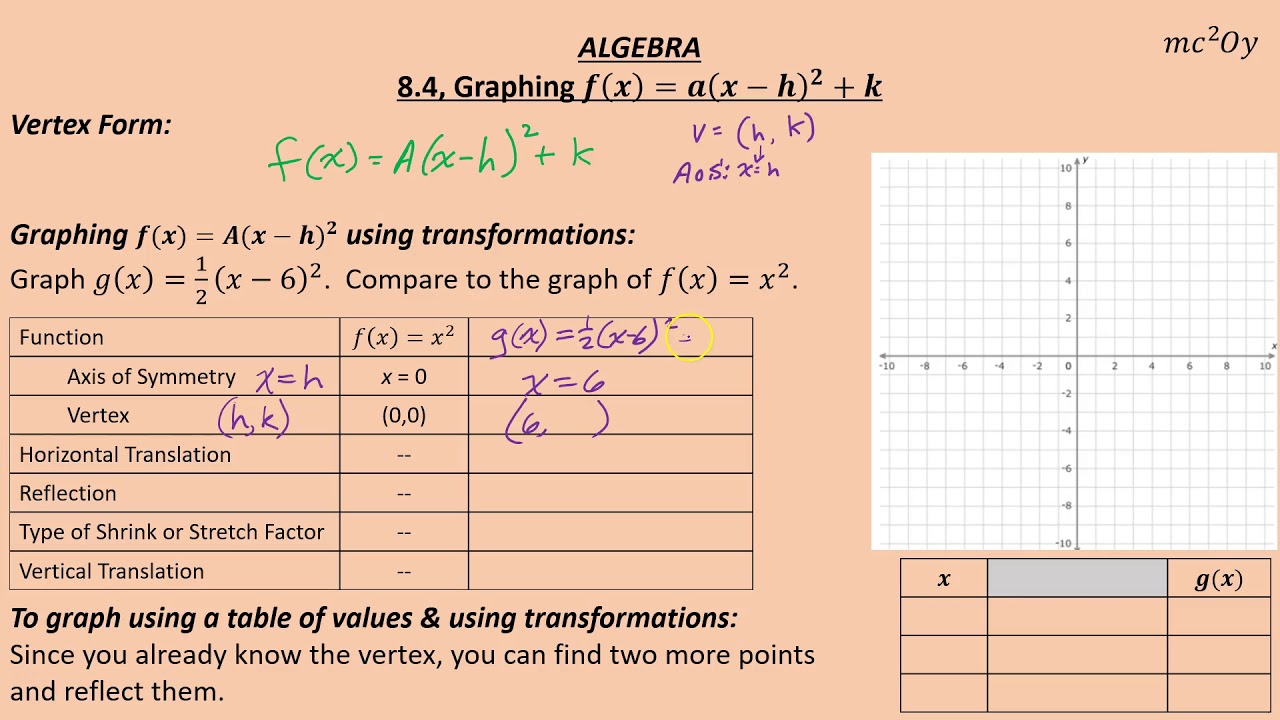



A 8 4 Graphing F X A X H 2 K Youtube



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
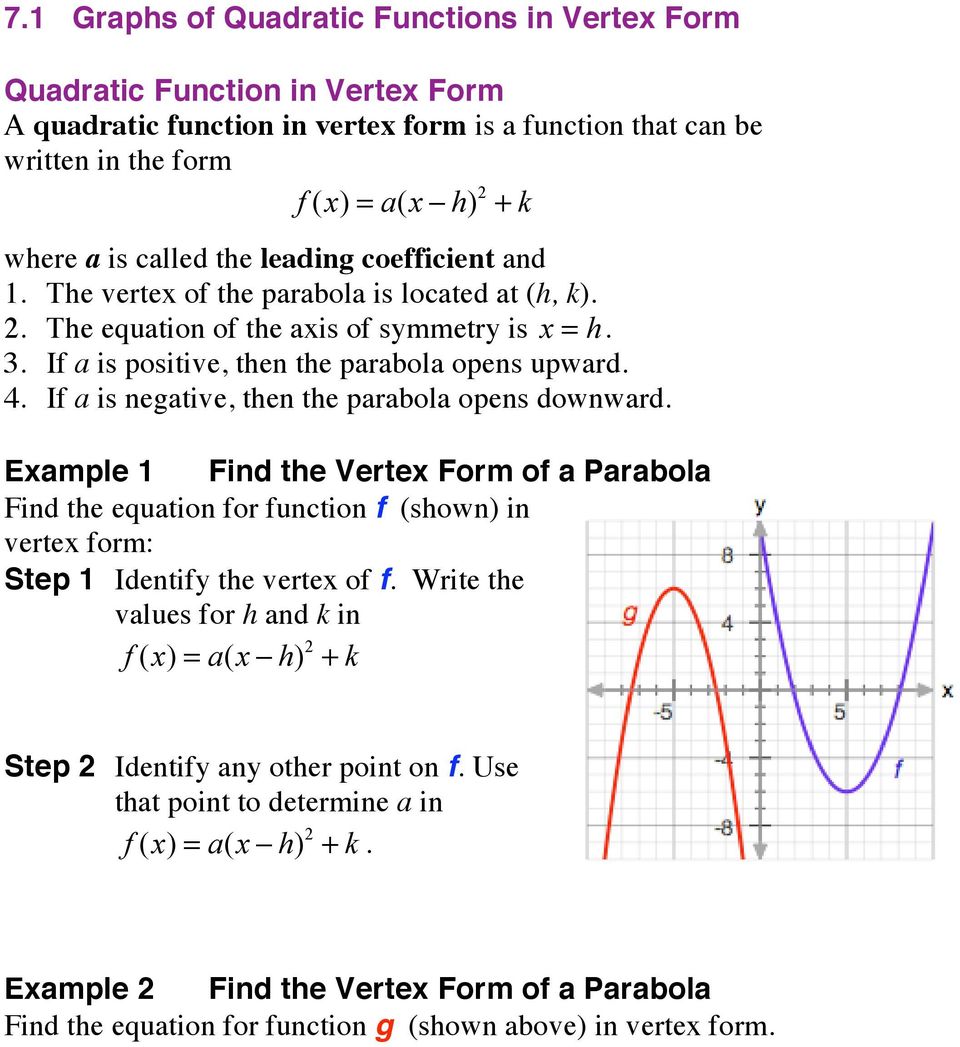



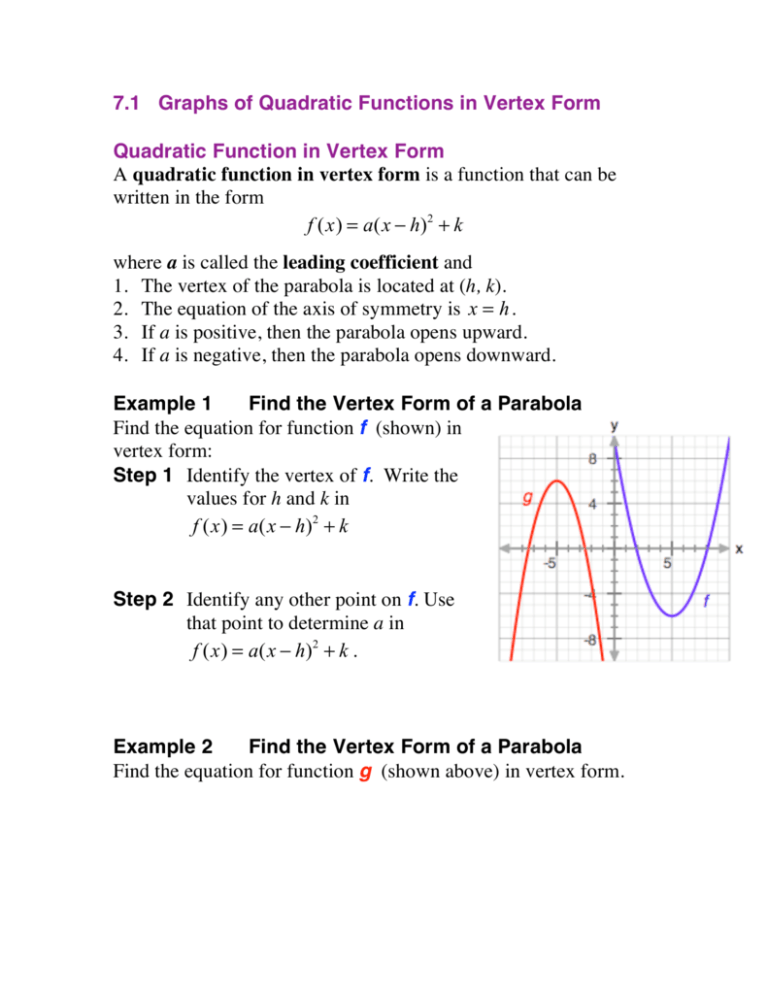
7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download
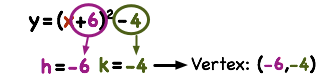



How Do You Convert A Quadratic From Standard Form To Vertex Form By Completing The Square Printable Summary Virtual Nerd
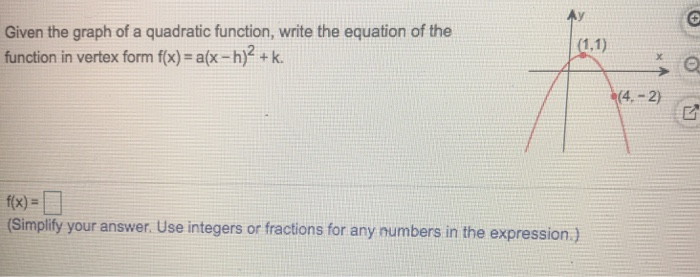



Given The Graph Of A Quadratic Function Write The Chegg Com



In The Following Exercises Write The Quadratic Function In F X A X H 2 K Form Whose Graph Is Shown Bartleby




Standard Form To Vertex Form Without Completing The Square Method Algebra 2 Youtube




Quadratic Functions




Graphing Parabolas




Quadratic Function Formulas Definition Graphs Examples




Write The Quadratic Function In The Form F X Chegg Com



The Quadratic Function F X A X H 2 K Is In Chegg Com




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21




Answered Create A New Function In The Form Y Bartleby




Identify The Vertex On No 6 Find An Equation Of The Parabola F X U 10 X Homeworklib



Answered Write The Quadratic Function In The Bartleby



Illustrative Mathematics



Transformations Of Absolute Value Functions Texas Gateway



Graphing Quadratic Functions



Solution Write The Given Expression In The Form F X A X H 2 K Identify The Vertex F X 6 5x 10x 2



Http Www Math Wsu Edu Faculty Dzhang 1fall14 1lecturenotes Fall14 Wed9 10 Pdf



Solved The Graph Shows G X Which Is A Translation Of F X X 2 Write The Function Rule For G X Write The Answer In The Form A X H 2 K Course Hero



Algebra 2 Vertex And Factored Form Of Quadratic Functions Algebra Ii Ti Math Nspired




Rewrite The Following Quadratic Functions In Chegg Com
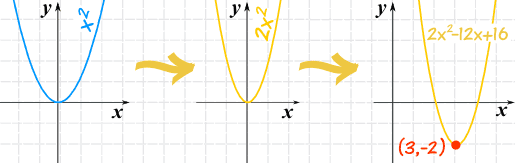



Graphing Quadratic Equations



Polynomial Functions Quadratic Functions Sparknotes




Quadratic Formula Calculator




Vertex Form Introduction Video Khan Academy




It S All In The Family Families Of Quadratic Functions
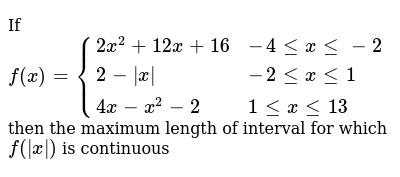



Please Help Write The Quadratic Function In The Form F X A



Q Tbn And9gcsupky3blzyvahq5luisbwmy5yqhhgberq0 Aopi9dy6e1gkiwi Usqp Cau



Illustrative Mathematics



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
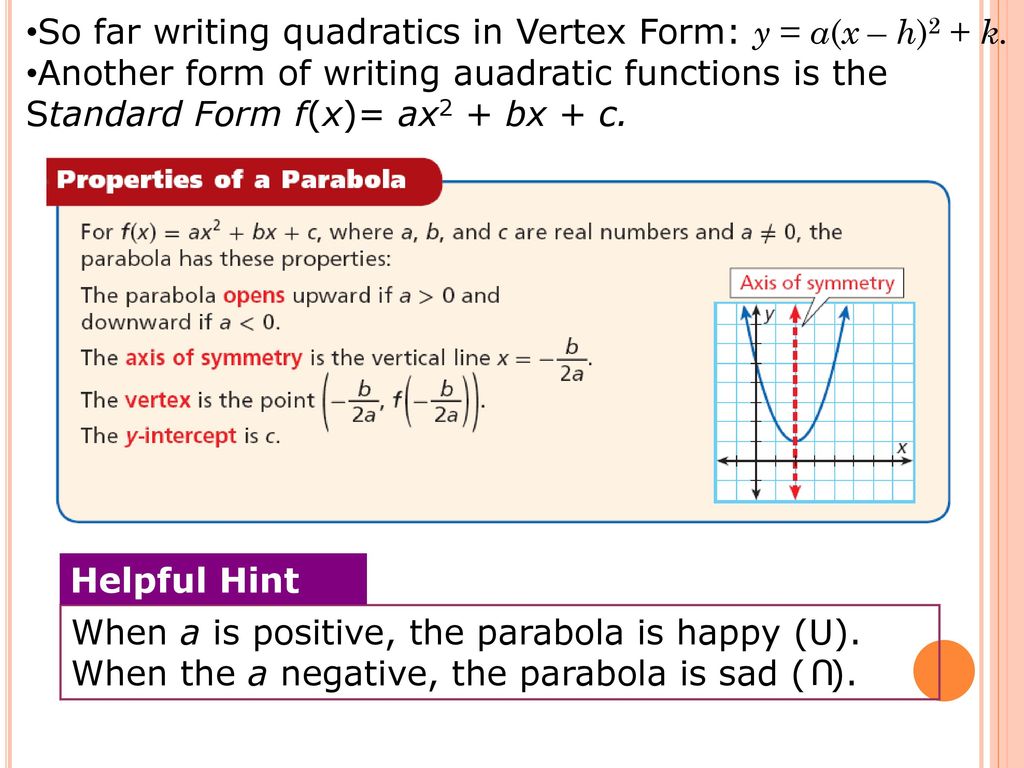



5 2 Properties Of Quadratic Functions In Standard Form Ppt Download




Vertex Intercept And Standard Form Read Algebra Ck 12 Foundation



Vertex Formula




Quadratic Functions




Determine The Quadratic Function Of The Form F X Chegg Com




Changing A Quadratic Function Into Vertex Form Youtube




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21




Unit 5 Quadratic Functions Flashcards Quizlet



F X A X H 2 K F X A X H 2 K F X A X H 2 K




Calgebra A1 8 4 Graphing F X A X H 2 K Youtube




Write The Quadratic Function In F X A X H 2 K Form Whose Graph Is Shown F X Brainly Com




Quadratic Function Wikipedia



5 2 Quadratic Functions Mathematics Libretexts



0 件のコメント:
コメントを投稿